Iterated cost modelling

The iterative cost model provides an alternative way of thinking about data and spectrum demand by treating data consumers and network operators as rational economic agents.  In other words, consumers adjust their consumption of data in response to unit cost and price changes (rather than simply demanding the same quantity of data regardless of the cost and price). On the supply side, operators expand network capacity as long as there is sufficient willingness to pay for the extra capacity.

One analogy of the iterative approach is road traffic planning.  Transport planners noticed that expanding road capacity did not solve the problem of congestion – instead, it increased the number of journeys until congestion was again a constraint. The extra road capacity lowered the ‘cost’ (in terms of time) of a car journey, so more car journeys were made. This model applies this idea to mobile data – in the model, data demand and supply react to changing market conditions.

The iterative approach incorporates a demand side assumption (consumers buy mobile data up to their willingness to pay) and a supply side investment decision rule, (only invest in capacity if willingness to pay for data exceeds the cost). The model is solved iteratively to find an equilibrium between data supply (capacity) and data demand as illustrated below.

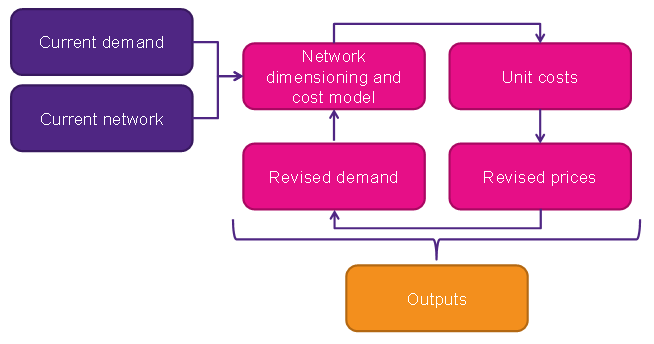
The core of the iterative cost model is similar to the avoided cost model, with a network dimensioning module calculating a network cost based on volumes and spectrum holdings.  However, the iterative cost model takes the output of this central module to work out how unit costs would change following a change in the model parameters (such as spectrum holdings, network utilisation, or spectral efficiency) and uses this to define how demand would be affected, and feeds this into the central module a second time.

This is repeated a number of times (either a set number, or until an equilibrium between data supply and demand is reached). Once an equilibrium is found, the impact of additional spectrum can be assessed, either by an avoided cost methodology (the additional spectrum reduces the cost of meeting the equilibrium level of demand) or by a consumer surplus methodology (the additional spectrum allows more data to be consumed, providing a benefit to consumers and society).

There are several advantages to using an iterative approach. Firstly, it removes the need for a data forecast as an input (although an assumption on per-user expenditure is required). Secondly, the iterative approach significantly reduces the sensitivity of the results to changes in the input parameters. Finally, the economic framework of the iterative approach means some of the insights produced are qualitatively different to those produced under conventional modelling approaches.